Area Related Circle Class 10 Formulas PDF

PDF Name	Area Related Circle Class 10 Formulas
No. of Pages	4
PDF Size	0.26 MB
Language	English
PDF Category	Education & Jobs
Source / Credits	files.pdfpdf.in
Uploaded By	Pradeep

Area Related Circle Class 10 Formulas - Summary

Getting comfortable with the Area related circle Class 10 formulas is really helpful for solving geometry problems easily. These formulas let you work out different measurements for circles, like their area, circumference, and the areas of sectors and segments. They’re important for doing well in your Class 10 Maths exams and are pretty easy to learn. To keep these important formulas handy for quick revision and exam prep in 2025, you can find the Area Related Circle Class 10 Formulas PDF download link at the bottom of this page.

Overview of Area Related Circle Class 10 Formulas PDF

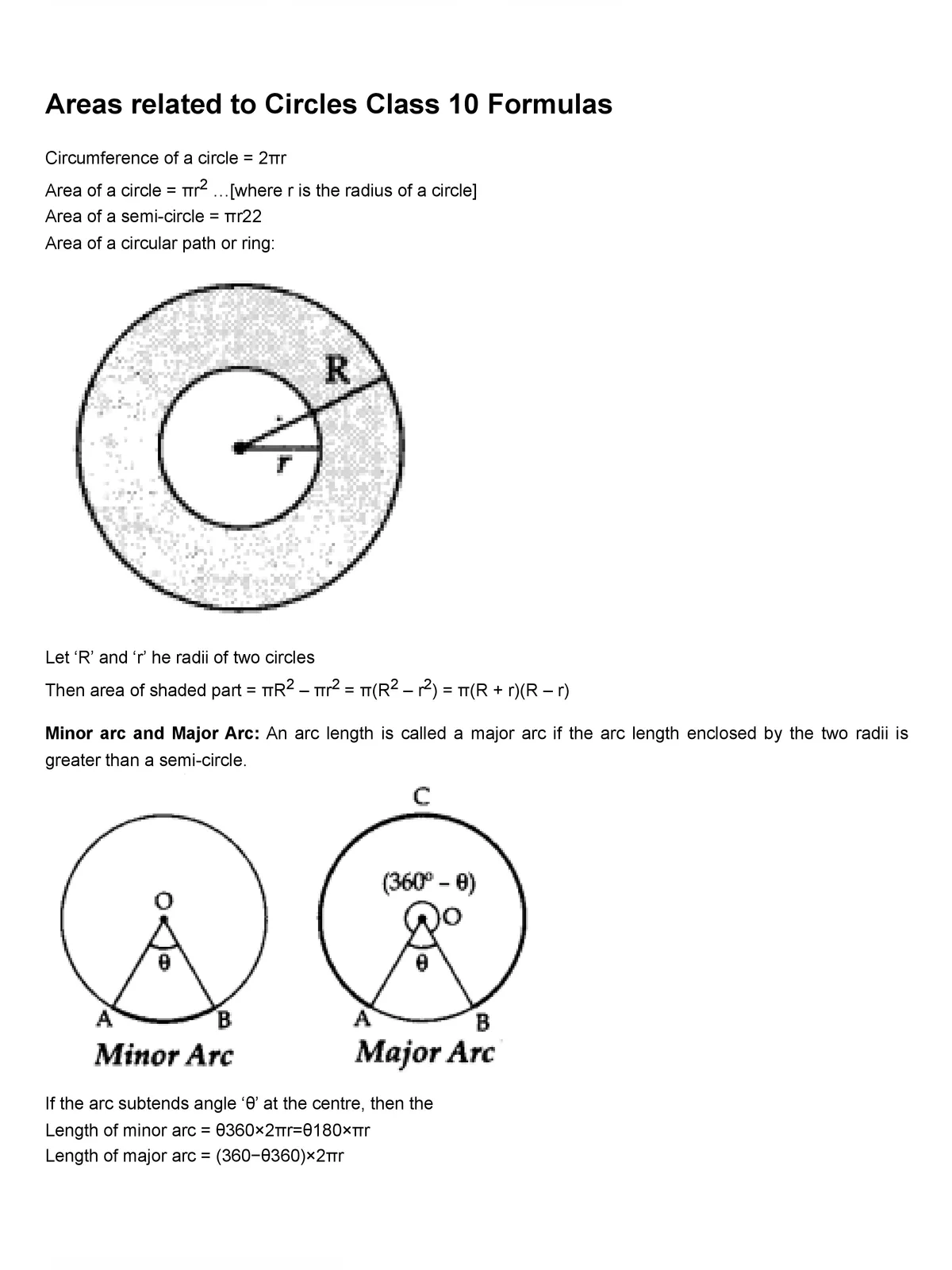
In the Class 10 Maths syllabus, Chapter 12 focuses on “Areas Related to Circles.” This chapter looks at the properties of the 2D circle shape and shows you how to calculate its area, circumference, arc length, and the areas of sectors and segments. A circle is basically a set of points that are all the same distance from a central point on a flat surface.

Main Formulas for Area Related Circle Class 10 You Should Know

Here’s a list of the main formulas you’ll use:

Circle Parameters	Formulas
Area of sector with angle b8	(b8/360) πr²
Length of arc of sector with angle b8	(b8/360) 2πr
Area of major sector	πr² – (b8/360) πr²
Area of segment of a circle	Area of corresponding sector – Area of corresponding triangle
Area of major segment	πr² – Area of minor segment

Detailed Explanation of Important Area Related Circle Class 10 Formulas

Let’s explain each formula with simple examples.

Area of a Circle Formula

You can find the area of a circle with the formula πr². Here, π (pi) is a constant usually taken as 22/7 or 3.14, depending on which makes the math easier. The letter ‘r’ stands for the radius of the circle.

π represents the ratio of a circle’s circumference to its diameter.

Example: Suppose you have a circle with a radius of 7 cm. To find its area:

Solution: Using the formula, Area = πr² = (22/7) 7² = (22/7) 49 = 22 7 = 154 square cm.

Circumference of a Circle Formula

The circumference is the total distance around the edge of a circle. It’s also called the perimeter of the circle and is given by the formula 2πr, where ‘r’ is the radius.

Example: Find the circumference of a circle with a radius of 21 cm.

Solution: Using the formula, Circumference = 2πr = 2 (22/7) 21 = 2 22 3 = 44 3 = 132 cm.

Area of a Sector of a Circle Formula

A sector of a circle is like a slice of pizza. Its area is found using the formula (b8/360) πr². In this formula, b8 is the angle formed by the two radii at the centre of the circle (in degrees), and ‘r’ is the radius.

Length of an Arc of a Sector Formula

The arc length of a sector is the length of the curved edge of the slice. It’s calculated with the formula (b8/360) 2πr, where b8 is the central angle of the sector and ‘r’ is the radius.

Area of a Triangle Formula

Sometimes, when working with segments, you’ll need the area of a triangle. The basic formula is (1/2) base height.

If the triangle is equilateral (all sides equal), its area is found using Area = (u221A3/4) a², where ‘a’ is the length of a side.

Area of a Segment of a Circle Formula

A segment of a circle is the area inside a chord and an arc. To find its area, subtract the area of the triangle formed by the radii and the chord from the area of the related sector.

Area of segment = Area of corresponding sector – Area of corresponding triangle

This can be written as: Area of segment = (b8/360) πr² – (1/2) base height.

If needed, you can use trigonometry (like sine and cosine) to find the base and height of the triangle.

An alternative formula when you know the angle b8 is:
Area of segment = (b8/360) πr² – r² sin(b8/2) cos(b8/2).

Having these Area related circle Class 10 formulas ready is very helpful for your exam preparation in 2025. Remember, you can easily download the Area Related Circle Class 10 Formulas PDF using the link below to keep all your learning and practice in one place.

RELATED PDF FILES