Integration Formulas PDF

Integration Formulas - Summary

Integration is a fundamental concept in mathematics that can be described as the reverse process of differentiation, or what we may refer to as Inverse Differentiation. Basically, integration involves finding a function whose derivative is known. This important process is not only essential for understanding calculus but also plays a crucial role in various real-life applications, such as determining areas of two-dimensional shapes and calculating the volumes of three-dimensional objects.

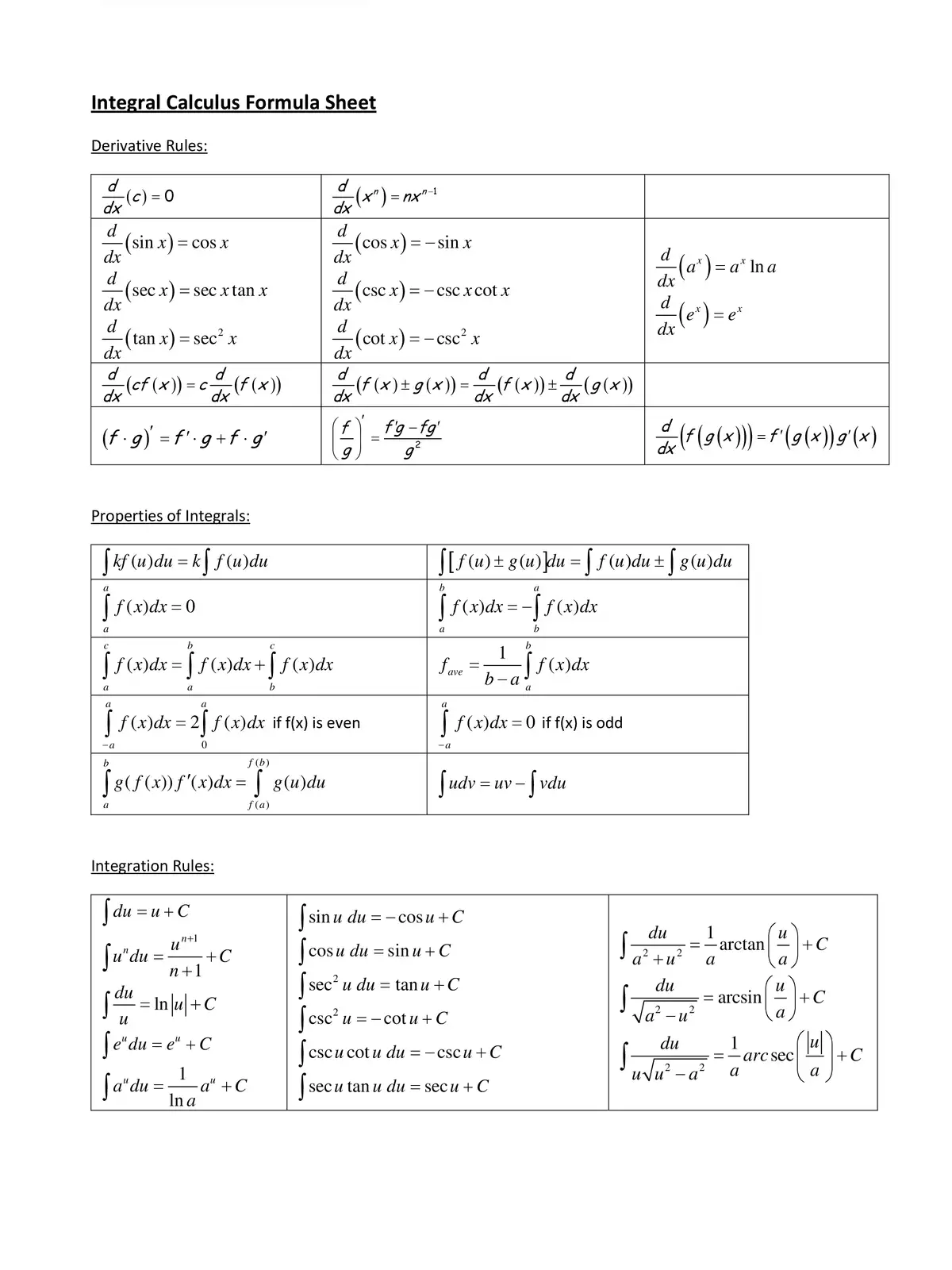
Integral Formulas

Here’s a list of some basic integral formulas that you should know:

• ∫ 1 dx = x + C
• ∫ a dx = ax + C
• ∫ xⁿ dx = ((xⁿ⁺¹) / (n+1)) + C ; n ≠ 1
• ∫ sin x dx = – cos x + C
• ∫ cos x dx = sin x + C
• ∫ sec² x dx = tan x + C
• ∫ csc² x dx = -cot x + C
• ∫ sec x (tan x) dx = sec x + C
• ∫ csc x (cot x) dx = -csc x + C
• ∫ (1/x) dx = ln |x| + C
• ∫ e^x dx = e^x + C
• ∫ a^x dx = (a^x/ln a) + C ; a > 0, a ≠ 1

Classification of Integral Formulas

We can classify integral formulas based on different types of functions, which include:

1. Rational functions
2. Irrational functions
3. Trigonometric functions
4. Inverse trigonometric functions
5. Hyperbolic functions
6. Inverse hyperbolic functions
7. Exponential functions
8. Logarithmic functions
9. Gaussian functions

For a comprehensive understanding, download the Integration Formulas PDF using the link given below.

RELATED PDF FILES

• Differentiation & Integration Formulas With Examples
• Integration Formulas With Examples
• 12th Maths Formulas List
• 50 Maths Formulas

Integration Formulas PDF Download